ITの世界では日々新しい技術が開発されるので、常に学び続けなければなりません。それに従い、学んだ技術が使えなくなることもあるのです。
ただし、コンピュータサイエンスの基礎に関しては、コンピュータを利用して技術が開発される限り、廃れるものではないので理解しておくと長期的に活用できるものだと思っています。
今回は2進数の足し算と引き算についてというテーマでお送りします。
そして、今回はこちらの本の勉強内容をアウトプットしています。
2進数の計算を理解する上で押さえておきたいコンピュータの仕組み
[kanren postid=”3937,3968,3986″]
以前、n進数間の基数変換への記事を書きました。
今回は2進数の足し算引き算についてというテーマでお伝えしていきたいと思っているのですが、まずはコンピュータの仕組みを押さえる必要があると考えています。
[kanren postid=”3894″]
こちらの記事でも書きましたが、コンピュータは、情報処理、データ処理、文書作成、音楽制作、写真編集、動画編集等という複雑な表現を0と1という2つの数字だけで表現しています。
その0と1という単純な数値しか利用しないということからイメージできると思うのですが、本来コンピュータは単純な処理しかできません。
そして、その単純な処理というのは足し算であり、実は引き算やかけ算やわり算も知らないんです。
理由としては回路をシンプルに保つためです。あれもこれもと詰め込むと経路が複雑になり処理が遅くなってしまいます。
でも、ぼくらが普段使うコンピュータは、それらの計算を難なくこなしてくれます。
その理由は、中に複雑な回路がなくとも解を出せる仕組みがあるからなのです。
以上のように、本来コンピュータは足し算のような単純な処理しかできないけれど、仕組みによって引き算やかけ算や割り算を行えるという点を、2進数の計算を理解するにあたって前提として押さえておきましょう。
2進数の足し算と引き算も基本は同じ
コンピュータは単純な処理しかできないということが分かった上で、2進数の足し算と引き算について考えていきたいと思います。
結論からお伝えすると、2進数の足し算と引き算の基本はぼくらが普段使っている10進数と変わりがないです。
ただ、例えば「10+4はいくつ?」「6-3はいくつ?」という普段から馴染みのある簡単な計算はできても、「101+10は?」「1001-101は?」という2進数の計算はすぐに瞬間的に答えられるものではないです。
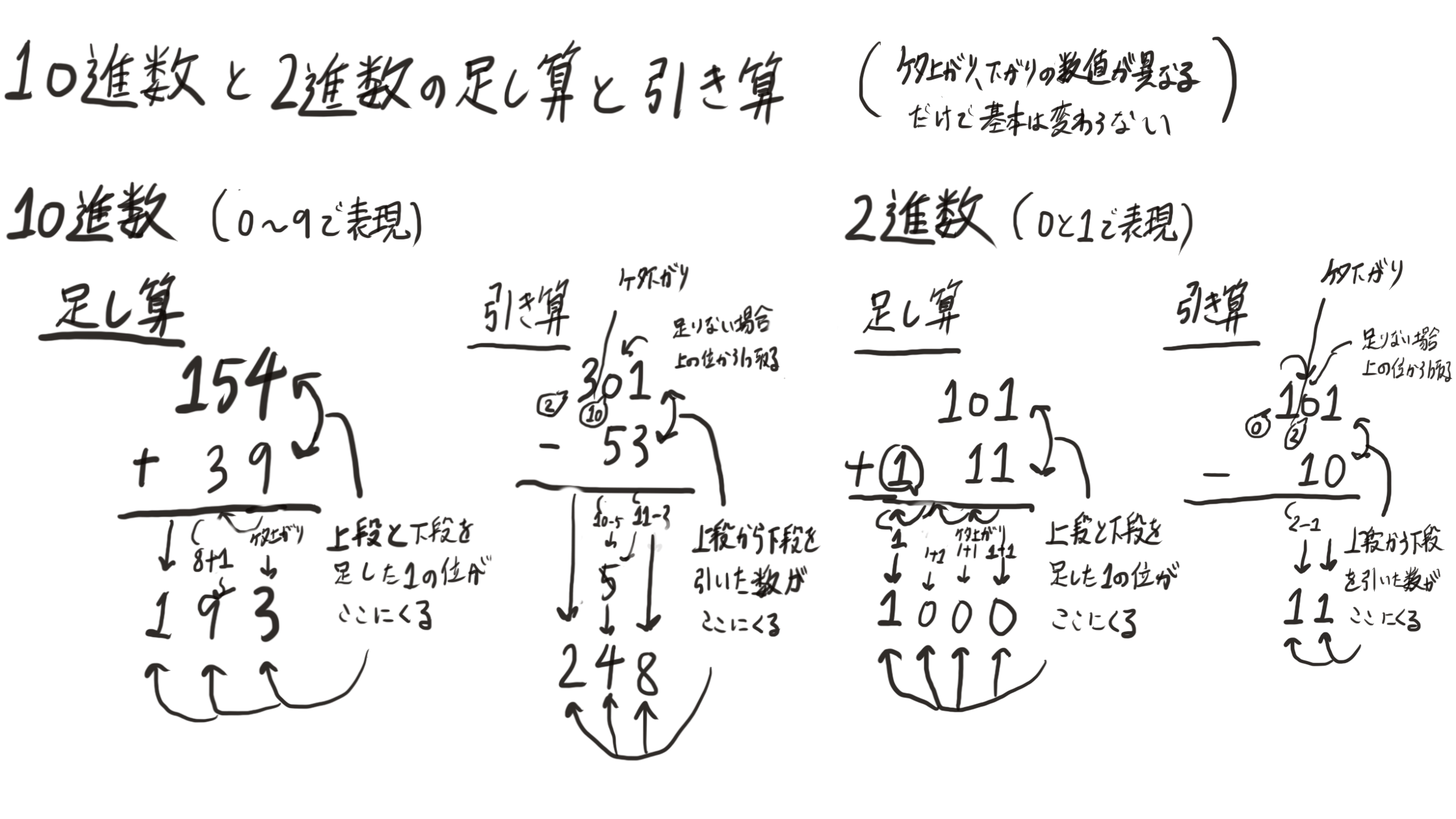
ですが、上の図をみていただければわかるように、10進数も2進数も桁が上がったり下がったりするときの数が異なるぐらいで基本は同じなのです。
しかし、シンプルに回路を構成するというコンピュータの特性に応じて、コンピュータには引き算という概念が載っていないのでどうやって引き算をするのかその仕組みを理解する必要があります。
2進数の引き算を理解する上で足し算をおさらいする
2進数の引き算を理解する上で欠かせないのが足し算に対する理解になります。
改めて、足し算だけにフォーカスをあててみて理解するためにも足し算の結果を見ていきます。
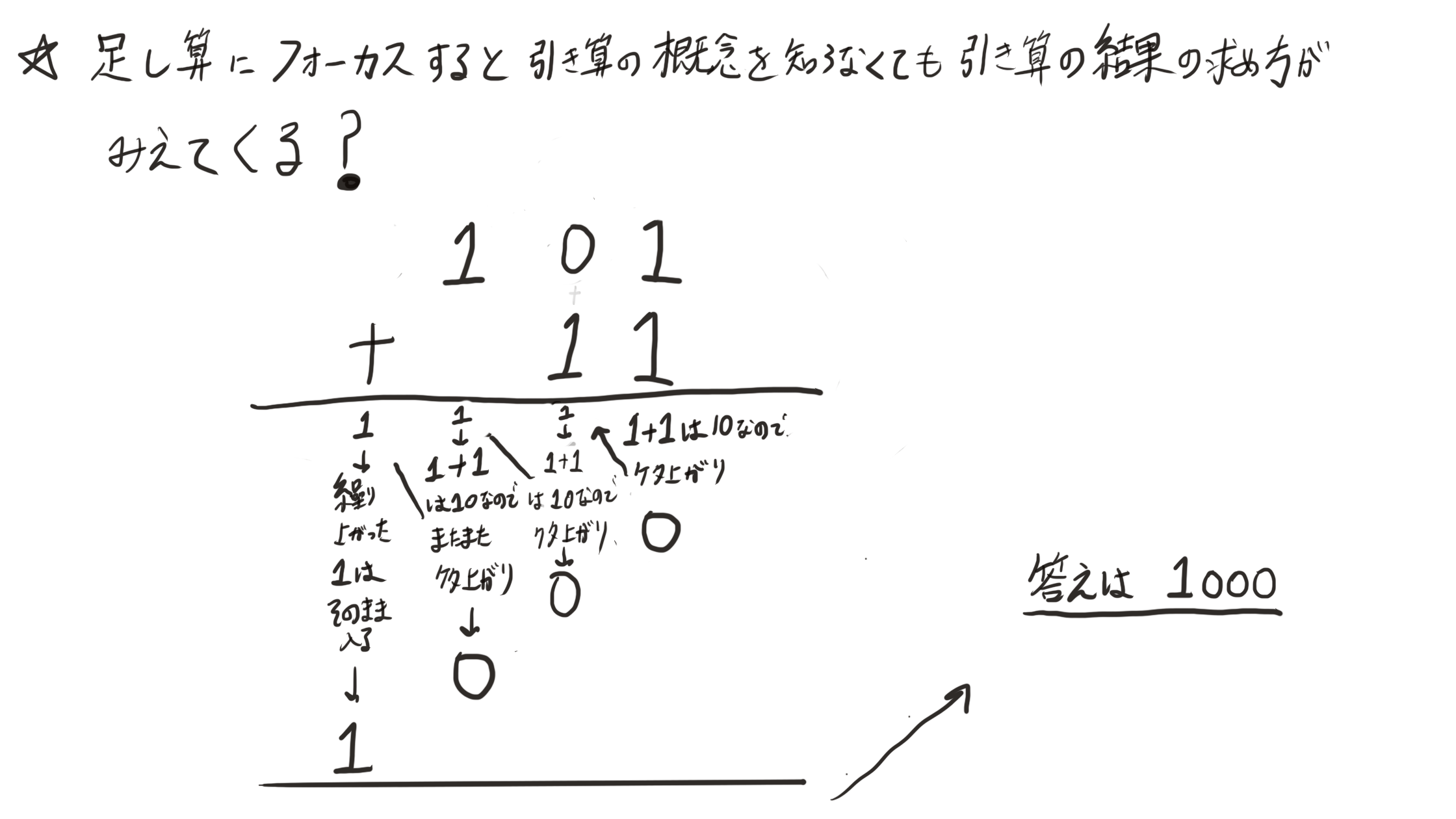
ここでクイズなのですが、元の数に戻すために11を引いたら101が表現できると思うのですが足し算で表現するとすればどうすればいいでしょうか?
このように、足し算にフォーカスした上で考えると引き算という概念がないものに引き算をさせる方法が見えてくるのではないでしょうか?
正解は、引き算ができないのなら、引き算と同じ結果を足し算で表現をすることを考えてみればよいのです。
例えば、2進数の「101-11」という計算をコンピュータにさせたい場合「101+(-11)」という計算ができれば引き算の概念を知らなくても足し算を使って引き算と同じ結果を得ることができます。
要はこの例の場合-11という負の数を表現することができれば足し算の回路だけで引き算で求める結果を得ることができるのです。
負の数を表現するために必要な補数とは?
単純に負の数が表せればいいと考えればやり方は様々です。

ただし、これでは足し算だけで引き算も行うという目的が達成できていません。
このときに負の数を表現するためにでてくるのが補数です。
補数は言葉の通り、補う数という意味です。
そして、その補数の種類には
[box class=”simple_box” title=”補数の種類”]
- その桁数での最大値を得るために補う数
- 次の桁に繰り上げるために補う数
[/box]
という2つの補数が存在します。
ただ文字だけみてもイメージが掴みにくいと思うので実際の数の例をつかって補数をみていきます。
10進数の補数
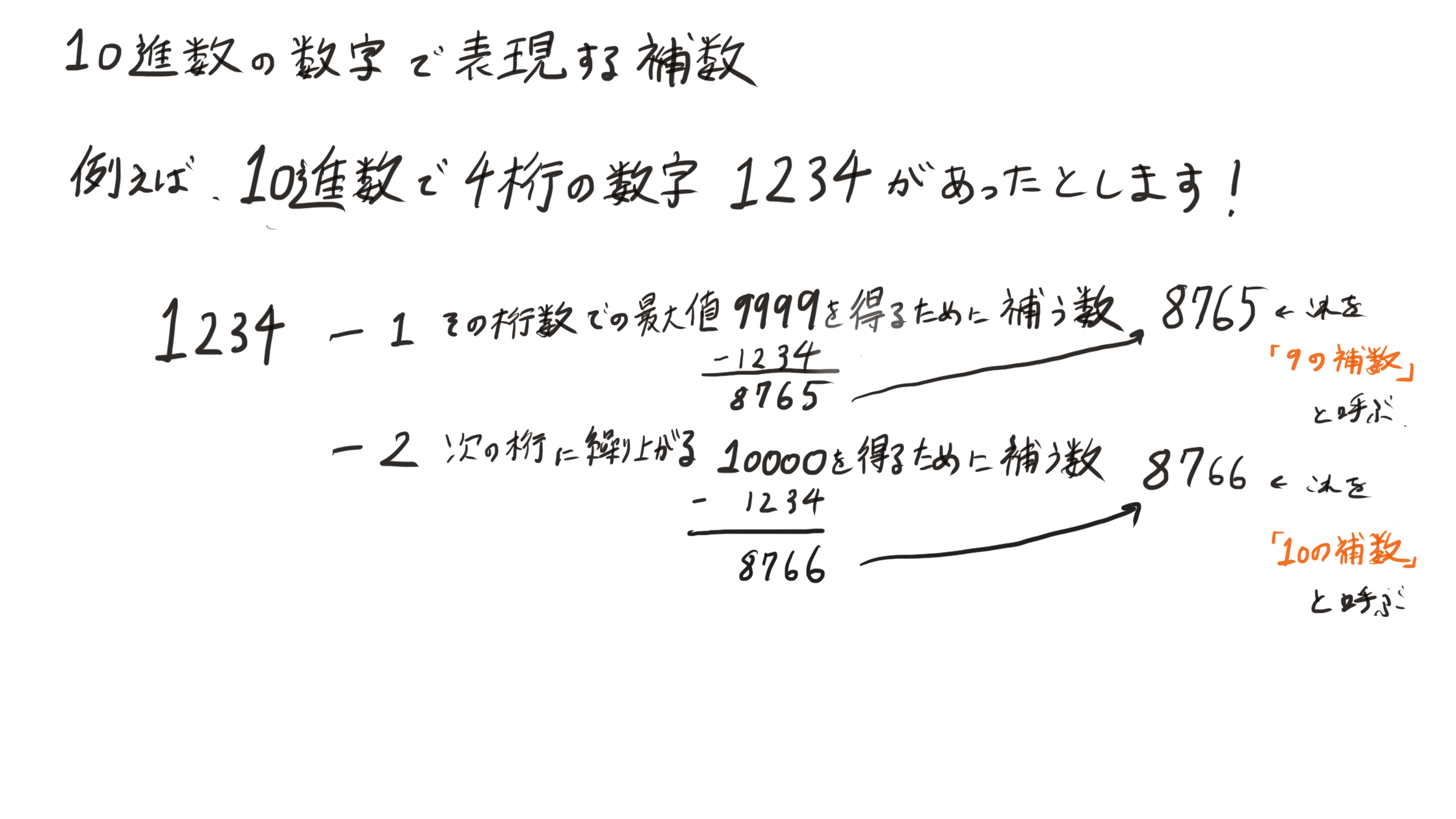
その桁数での最大値を得るために補う数が「9の補数」、次の桁に繰り上げるために補う数「10の補数」と呼びます。
2進数の補数
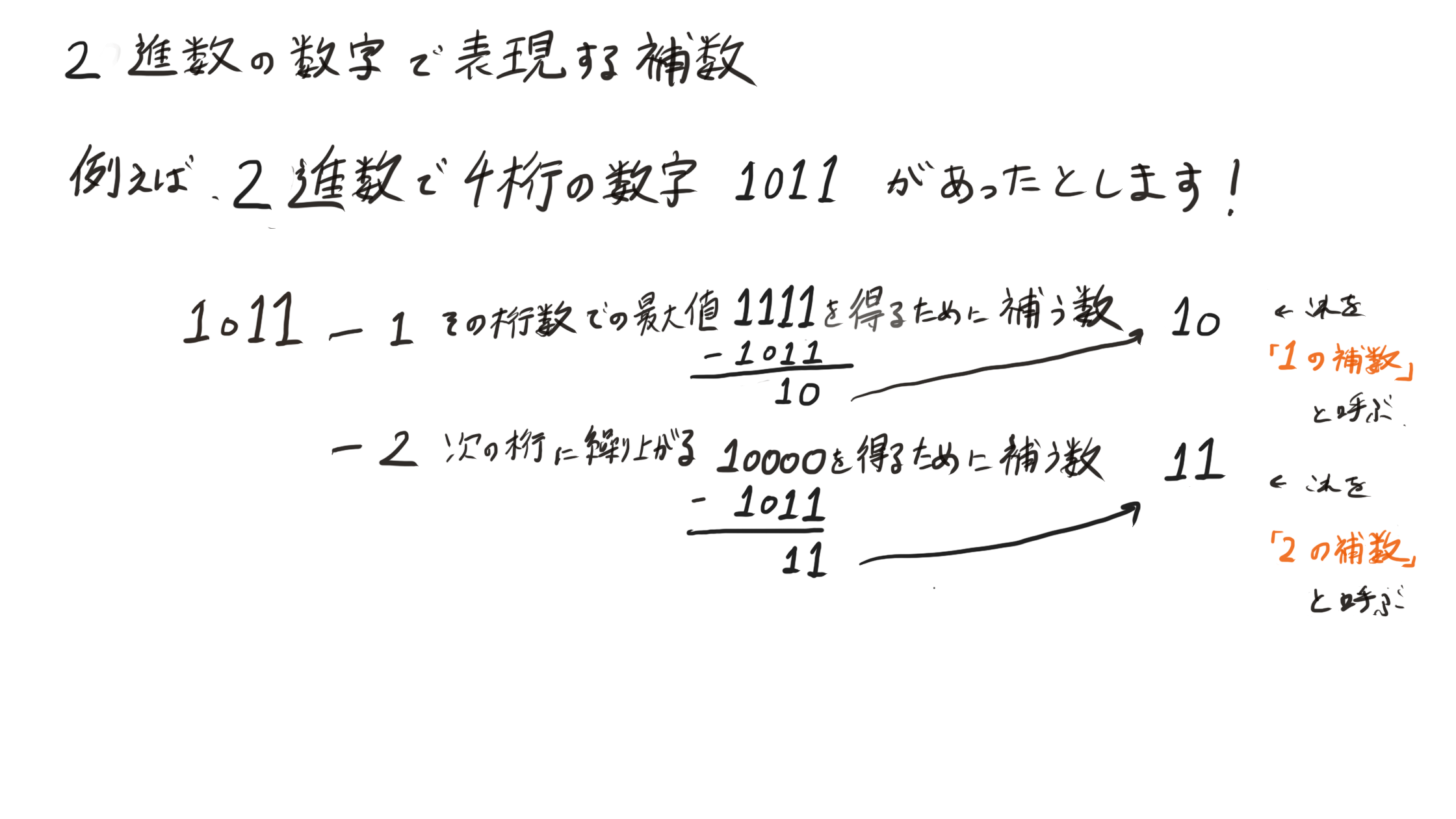
2進数では、10進数でいうところの「9の補数」と「10の補数」と同じものが、2進数にもあるわけです。
2進数では「1の補数」、「2の補数」と呼びます。
コンピュータで負の数を表すには2の補数を利用する
補数の種類を理解した上で、先ほどの8ビットの2進数の5に対し、その数の2の補数を加えてみます。
すると、2の補数のため当たり前なのですが、桁上がりした数になります。
このとき、8ビット部分から溢れ出てしまった9ビット目を無視して8ビット部分だけを見れば全部0、つまり足し算した結果は0とみなしてあげることができるのです。
このように、ある数値に対する2の補数表現は、そのままその数値の負の値として使えます。
このことから、コンピュータは負の数を表現するのに2の補数を使います。
2の補数は次の手順で簡単に求めることができます。
[box class=”simple_box” title=”2の補数の求め方”]
- 全てのビットを反転させてあげる
- そこにたいして1を加算する
[/box]
2の補数を求める手順をインプットしておきましょう。
2進数の引き算の流れ
それでは、実際に例を用いて、引き算の流れを見てみることにします。
ここでは、2進数の「111」-「10」という式の場合の流れを確認してみましょう。
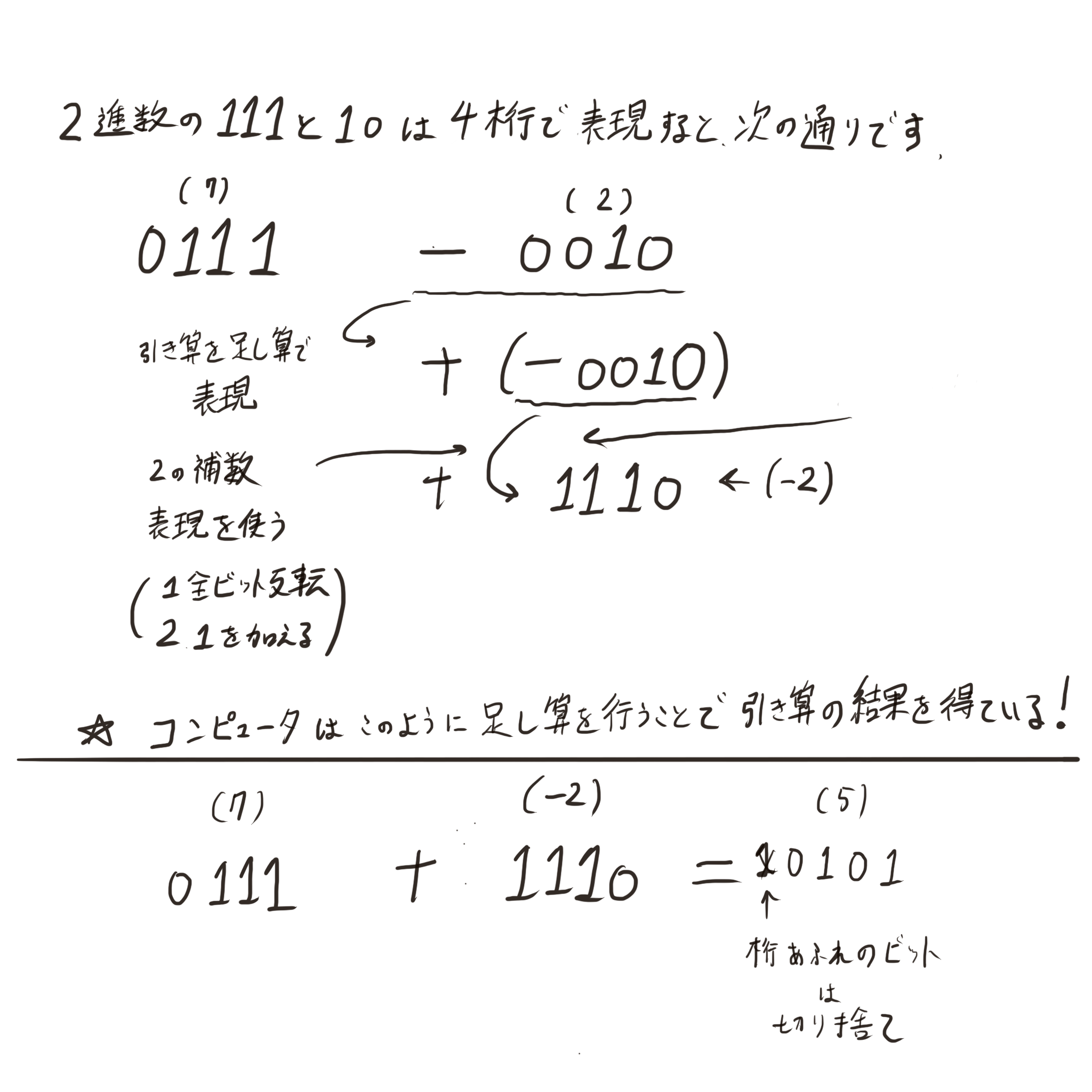
また、2の補数を用いて負の数を表す場合も1ビット目は符号として扱うことができます。
そして、正の数と負の数は互いに2の補数表現となる関係にあります。
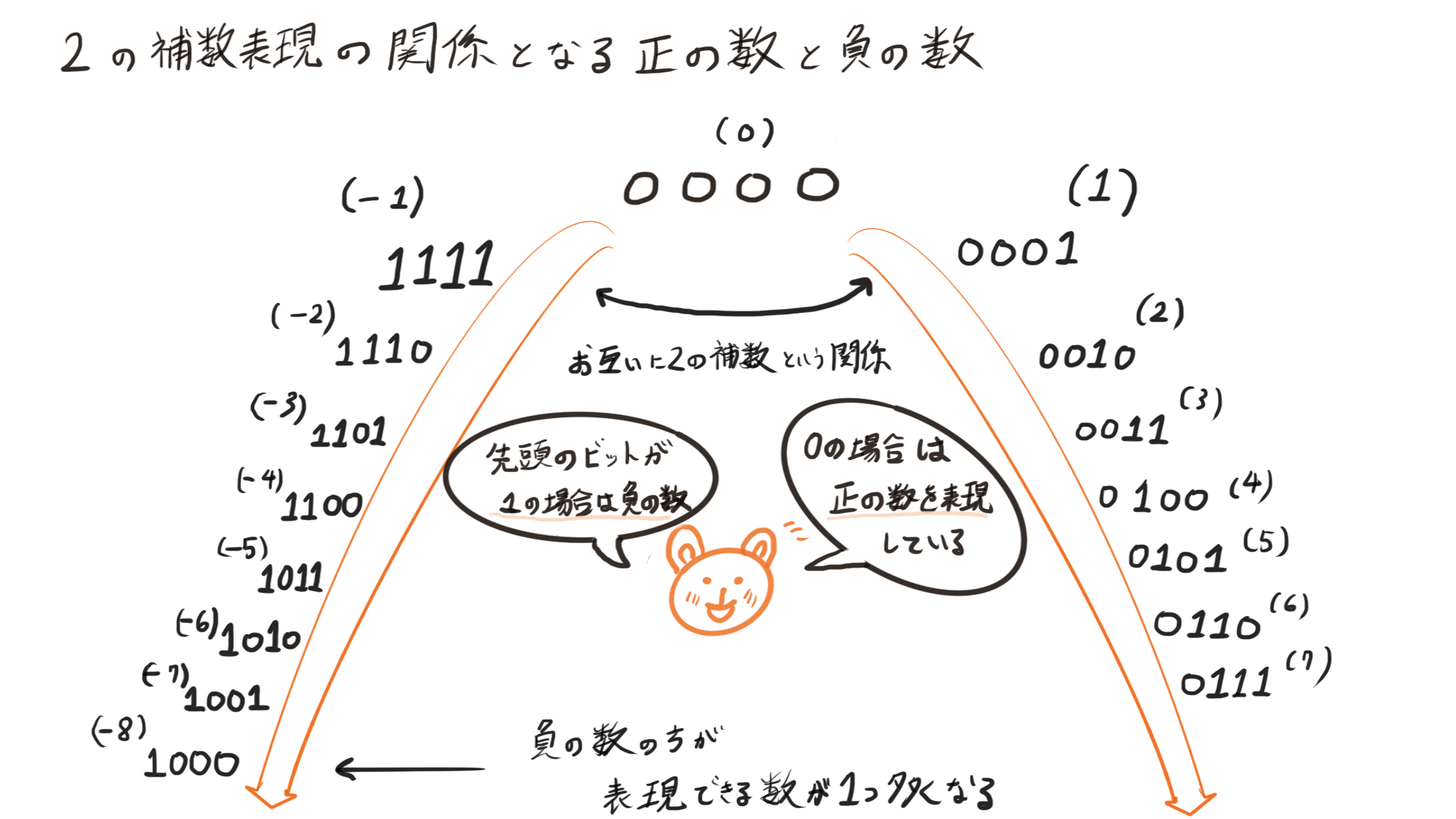
この関係で、負の数の方が表現できる数が1つ多くなるのでその点覚えておきましょう。
最後に

本日は2進数の足し算と引き算についてというテーマでお送りしました。
冒頭にも紹介しましたが、今回の内容に関しては以下の本で学ばせてもらったことを参考にアウトプットさせていただいています。
こちらは基本情報技術者試験の参考書となっていますが、ITサイエンスの基礎を学んでいく上でおすすめの本です。
Amazon内の評価も高く、他にも参考書はありますが、文章メインではなくイラストが多用されているので、特に初学者の方にはとっつきやすく理解しやすいと思います。
ぼくもこの本にかなりお世話になっていて、おすすめできる書籍となっているので、気になる方はぜひ手にとってみてください。
それでは本日もありがとうございました。
今日も頑張ります。
[kanren postid=”3968,3894,3924,3937,3951″]
