ITの世界では日々新しい技術が開発されるので、常に学び続けなければなりません。それに従い、学んだ技術が使えなくなることもあるのです。

ただし、コンピュータサイエンスの基礎に関しては、コンピュータを利用して技術が開発される限り、廃れるものではないので理解しておくと長期的に活用できるものだと思っています。

今回は基数と桁の重みについてというテーマで紹介します。

また、今日紹介する内容はこちらの本を参考にアウトプットさせていただいています。

基数と桁の重みとは

以前、n進数とは何かという記事について書きました。

[kanren postid=”3907″]

記事の中で、n進数はnの数字で桁上がりして表現する数だと説明したのですが、そのn進数には基数という概念があります。

これは要するに基本となる数のことを示します。

例えば、2進数であれば2、10進数なら10って感じでn進数のnにあたる数字が基数です。

そして、桁上がりする数字に着目してみると、1という数字が１桁桁上がりして左へ移動するごとに倍々ゲームで値が増えている法則がみえてくるのではないでしょうか。

 

これを各n進数が持つ各桁の重みといいます。

例えば、２進数なら1桁目は2の0乗、2桁目は2の1乗と桁ごとに「2の(桁数-1)乗」を行った数値、すなわち基数を累乗した数値が各桁の重みの正体となっているわけです。

n進数が持つ各桁の重みの法則を理解するメリットについて

n進数が持つ各桁の重みというのは、下図のような法則で決まっています。

 

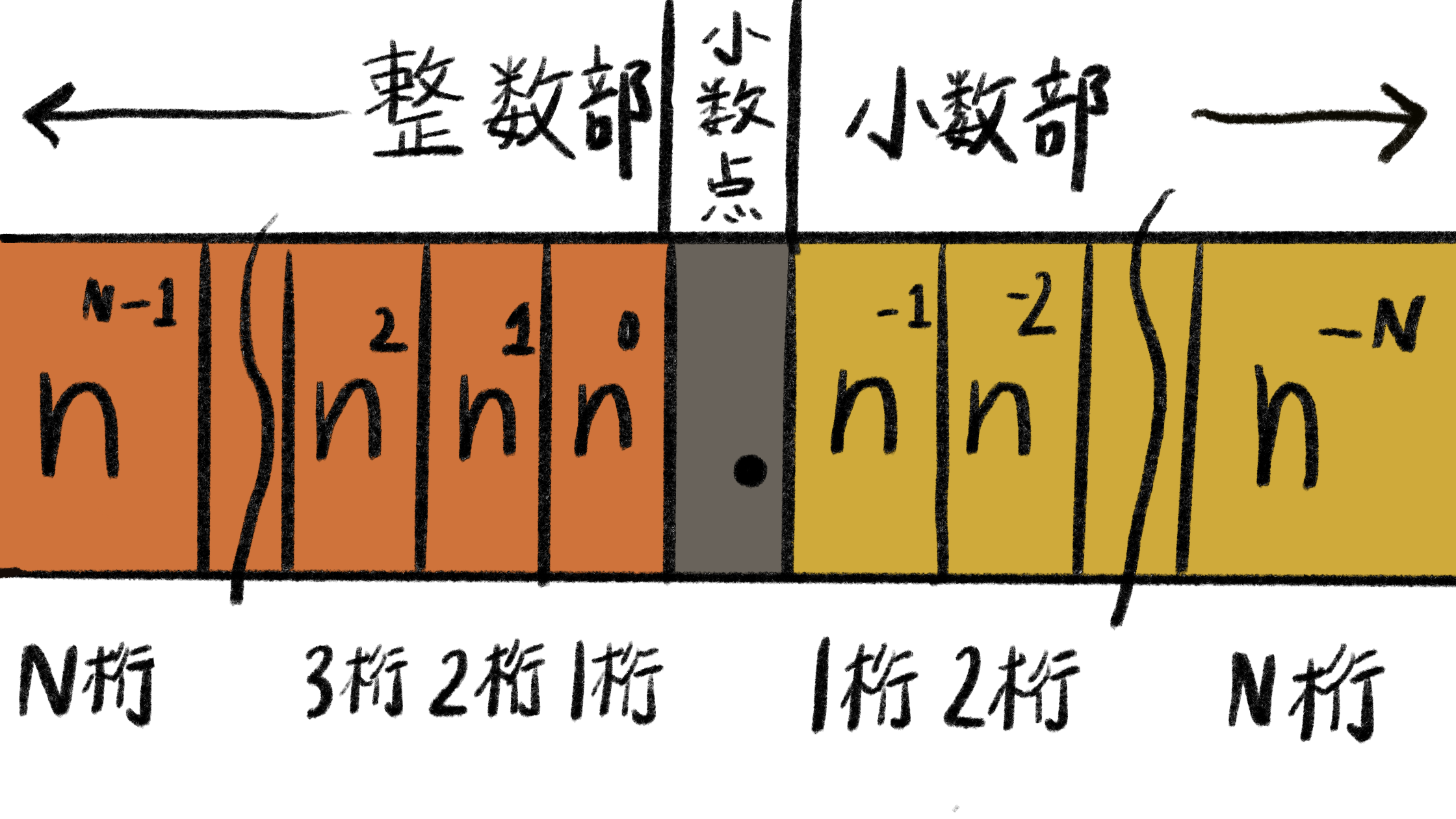
これにあてはめて考えるとそれぞれのn進数が持つ各桁の重みは次のようになります。

 

 

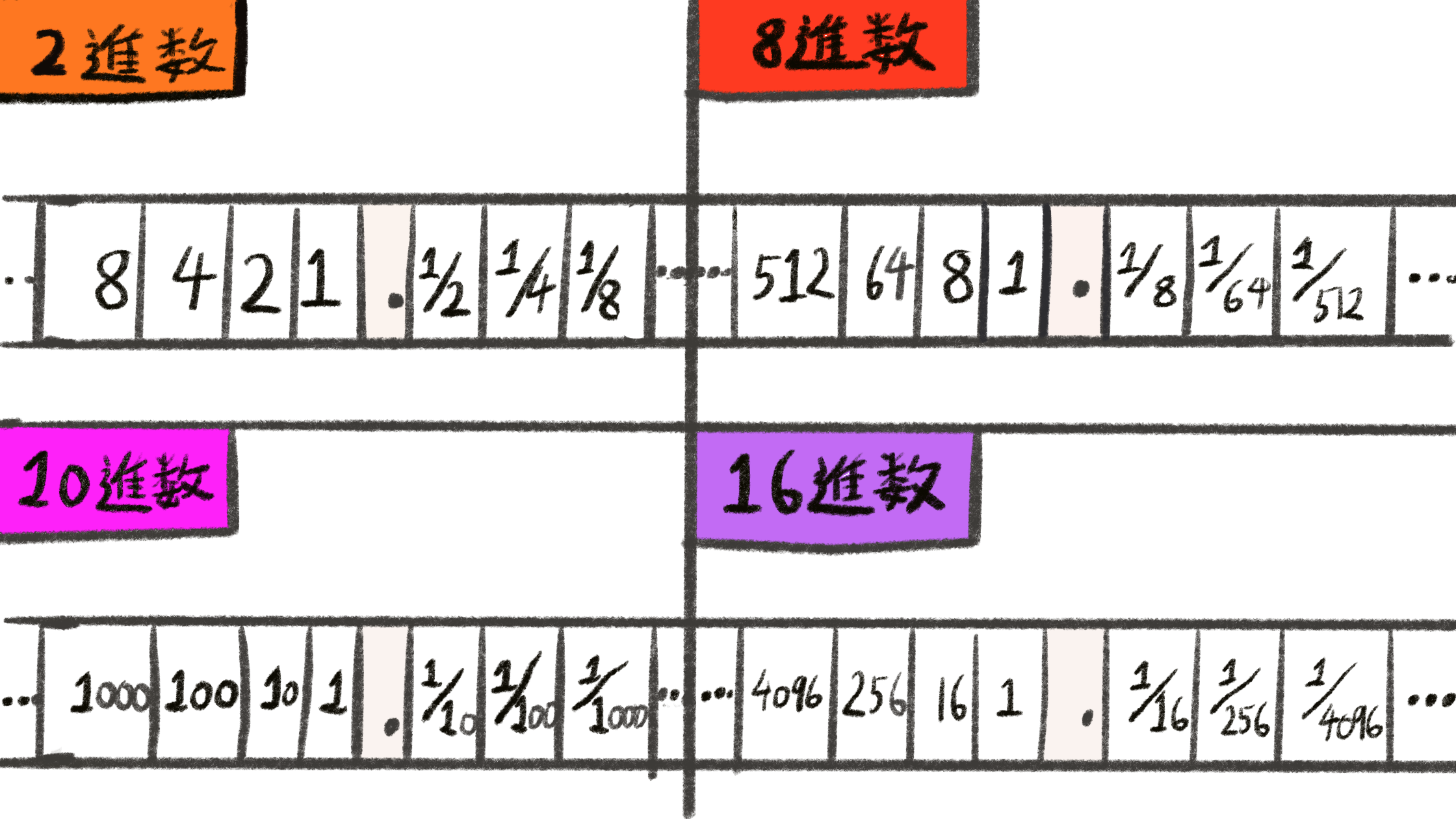
この各桁の重みの法則を理解できるようになると、基数と基数の変換をする際に役立ちます。

例えば、1010.010という2進数を10進数に変換するとします。100や1000などの２進数はすぐに10進数として表せるかもしれませんが、この1010.010をいちから計算するとしたらいくら時間があっても足りないですよね。

そんな、1010.010という複雑な２進数は、各桁の数字にその桁の重みを掛け算した数を合計することで容易に10進数表記における値が求められます。

 

 

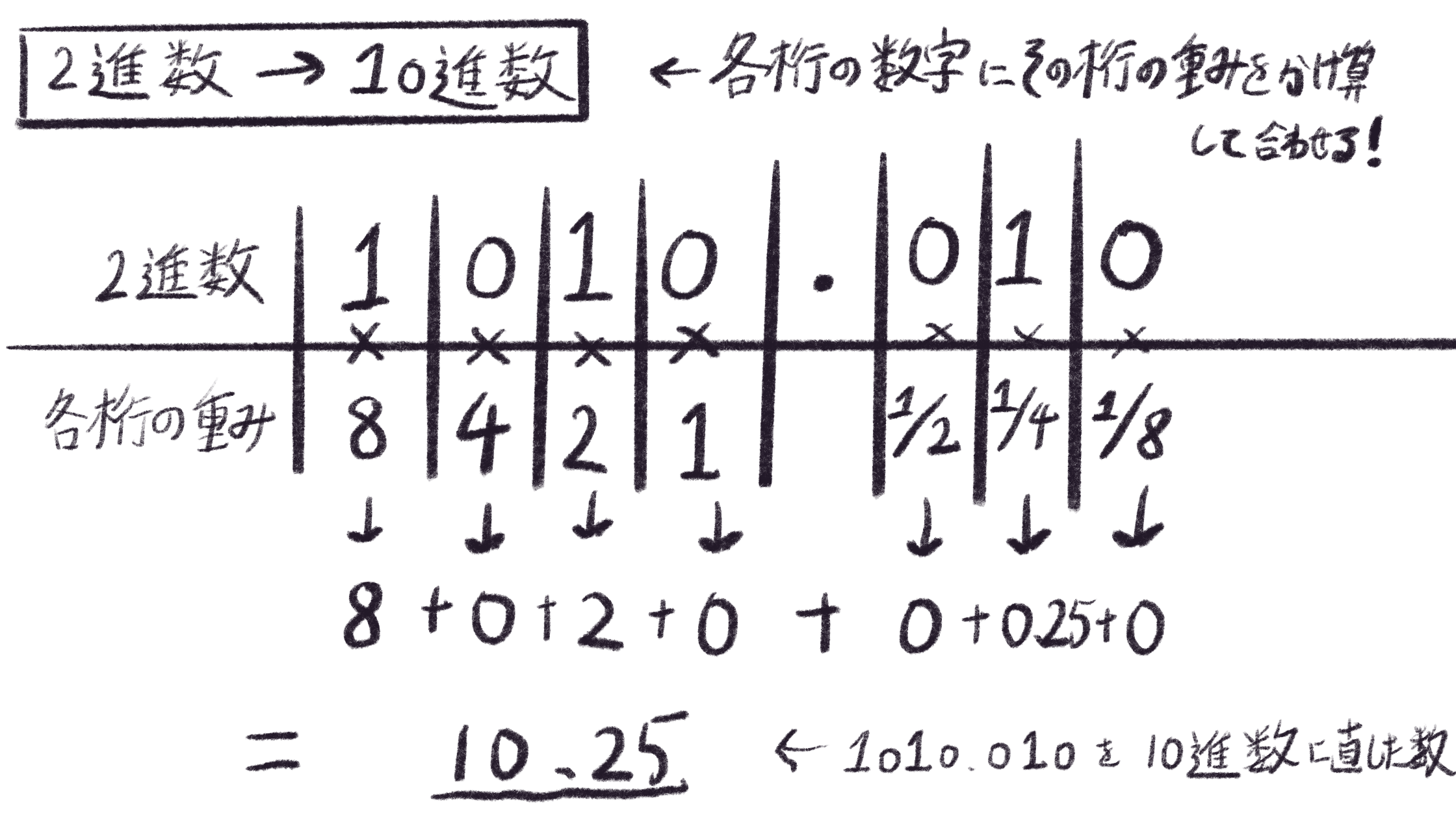
どうですか？桁の重みの法則を理解できるといちからやると大変だと思った基数変換が容易にできるとイメージできたのではないでしょうか。

今回は２進数から10進数への変換を紹介しましたが、他の基数変換も各基数の桁の重みを用いると容易にできるようになるため、この各桁の重みの法則は必ず理解しておきましょう。

最後に

本日は基数と桁の重みというテーマでお送りしました。

冒頭にも紹介しましたが、今回の内容に関しては以下の本で学ばせてもらったことを参考にアウトプットさせていただいています。

 

 

こちらは基本情報技術者試験の参考書となっていますが、ITサイエンスの基礎を学んでいく上でおすすめの本です。

Amazon内の評価も高く、他にも参考書はありますが、文章メインではなくイラストが多用されているので、特に初学者の方にはとっつきやすく理解しやすいと思います。

ぼくもこの本にかなりお世話になっていて、おすすめできる書籍となっているので、気になる方はぜひ手にとってみてください。

 

それでは本日もありがとうございました。

 

 

今日も頑張ります。

 

[kanren postid=”3894,3924″]