ITの世界では日々新しい技術が開発されるので、常に学び続けなければなりません。それに従い、学んだ技術が使えなくなることもあるのです。
ただし、コンピュータサイエンスの基礎に関しては、コンピュータを利用して技術が開発される限り、廃れるものではないので理解しておくと長期的に活用できるものだと思っています。
今回はシフト演算と2進数のかけ算とわり算についてというテーマでお送りします。
そして、今回はこちらの本の内容を参考にアウトプットしています。
シフト演算を理解して、2進数のかけ算や割り算を理解する
前回の記事で、コンピュータは単純な処理しかできないため、足し算以外の引き算やかけ算や割り算を知らないということをお伝えしました。
[kanren postid=”4003″]
それに従い、引き算の結果を求めるためには、足し算で2の補数を利用して負の数を表現する必要がありました。
もちろん、コンピュータは今回紹介する掛け算や割り算も知らないので、かけ算や割り算の結果を求めるためには中の操作を理解する必要があります。
その理解する必要のある操作はシフト演算です。
シフト演算とは2進数をあらわすビット列を、左もしくは右にずらす操作のことを指します。
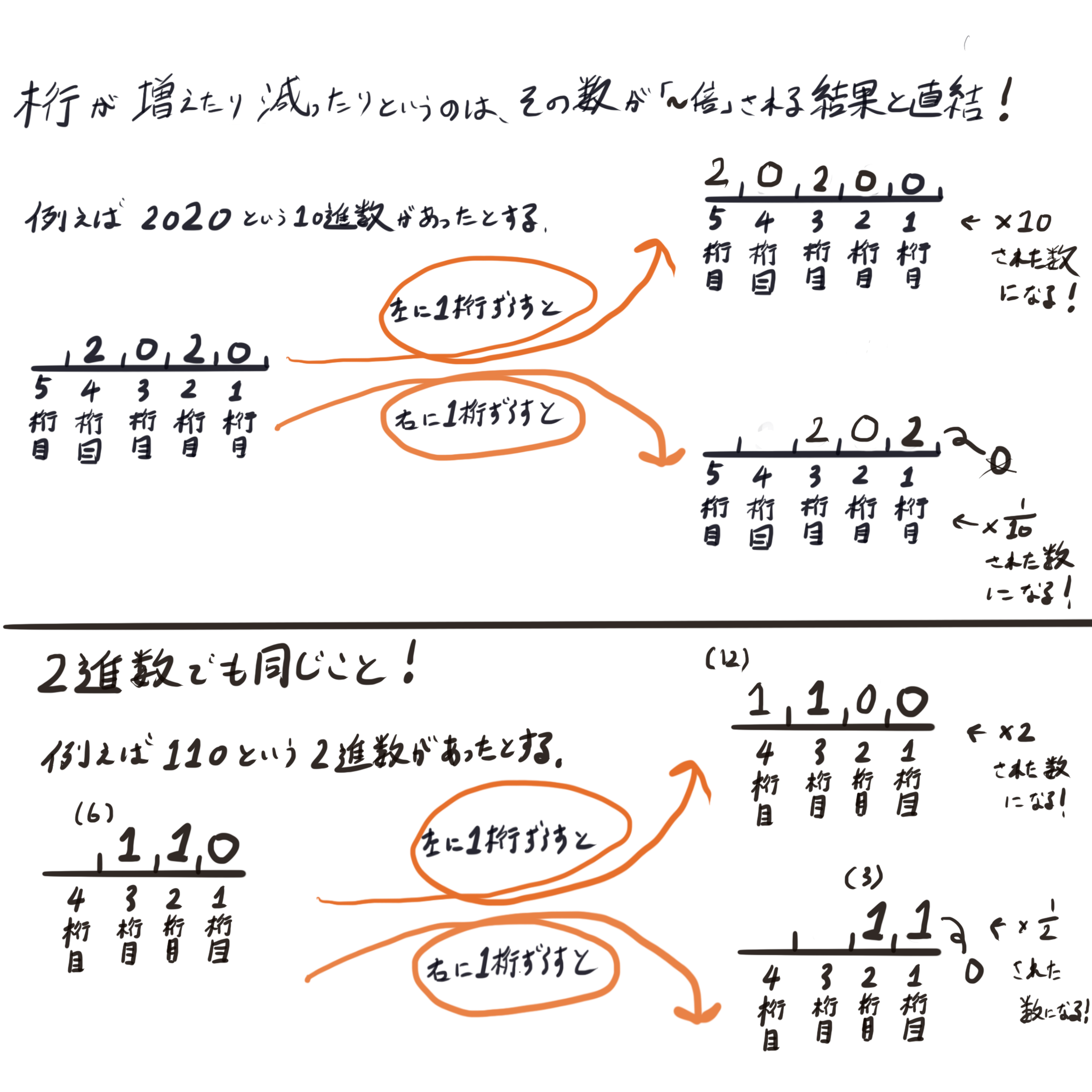
例えば、10進数2020という数字に対して「10倍」とか「1/10倍」するとどうなるかというとすぐに答えが出てきますよね。
10倍であれば20200ですし、1/10倍すれば202。
2進数でも同じことが言えて、例えば、2進数110を2倍すると1100、1/2倍すると11。
何も難しいことはありません。
このように桁が増えたり、減ったりするのはその数が〜倍されるという結果と直結しています。
この「~倍」の~にどんな数字が入ることになるかというと、
[kanren postid=”3937″]
こちらの記事で説明した基数と桁の重みに従って決まります。
したがって、10進数であれば桁の増減によって「10倍」「1/10倍」、2進数であれば「2倍」もしくは「1/2倍」になります。
そして、コンピュータはビットの並びを2進数として扱います。つまり、この並びをまとめて左にずらしたりすることや右にずらしたりすることで元の値の2倍や1/2倍という計算を行うのです。
この操作をシフト演算と呼び、コンピュータはこれを利用してかけ算やわり算の結果を導き出しています。
2種類のシフト演算
シフト演算はビットをずらすことによって計算を行なっているということを先ほど説明しました。
ちなみに、左にずらすことを左シフト。右にずらすことを右シフトと呼びます。
そして、このシフト演算にはシフトしたビットの結果が異なる2種類のシフトがあります。
[box class=”simple_box” title=”シフト演算の種類”]
- 論理シフト
- 算術シフト
[/box]
以上2種類の、それぞれのシフト演算の操作の特徴をみていきましょう。
論理シフト
まず、論理シフトは、符号を考慮せずに行うシフト操作です。
符号を考慮しないというのは、最上位のビットも含めて何も考えずにシフトをすることになります。
左論理シフト
符号を考慮せずにビット列全体を左にずらすのが左論理シフトです。
ずらしたビット数をnとすると、シフト後の数は元の数を2ⁿ倍したものになります。
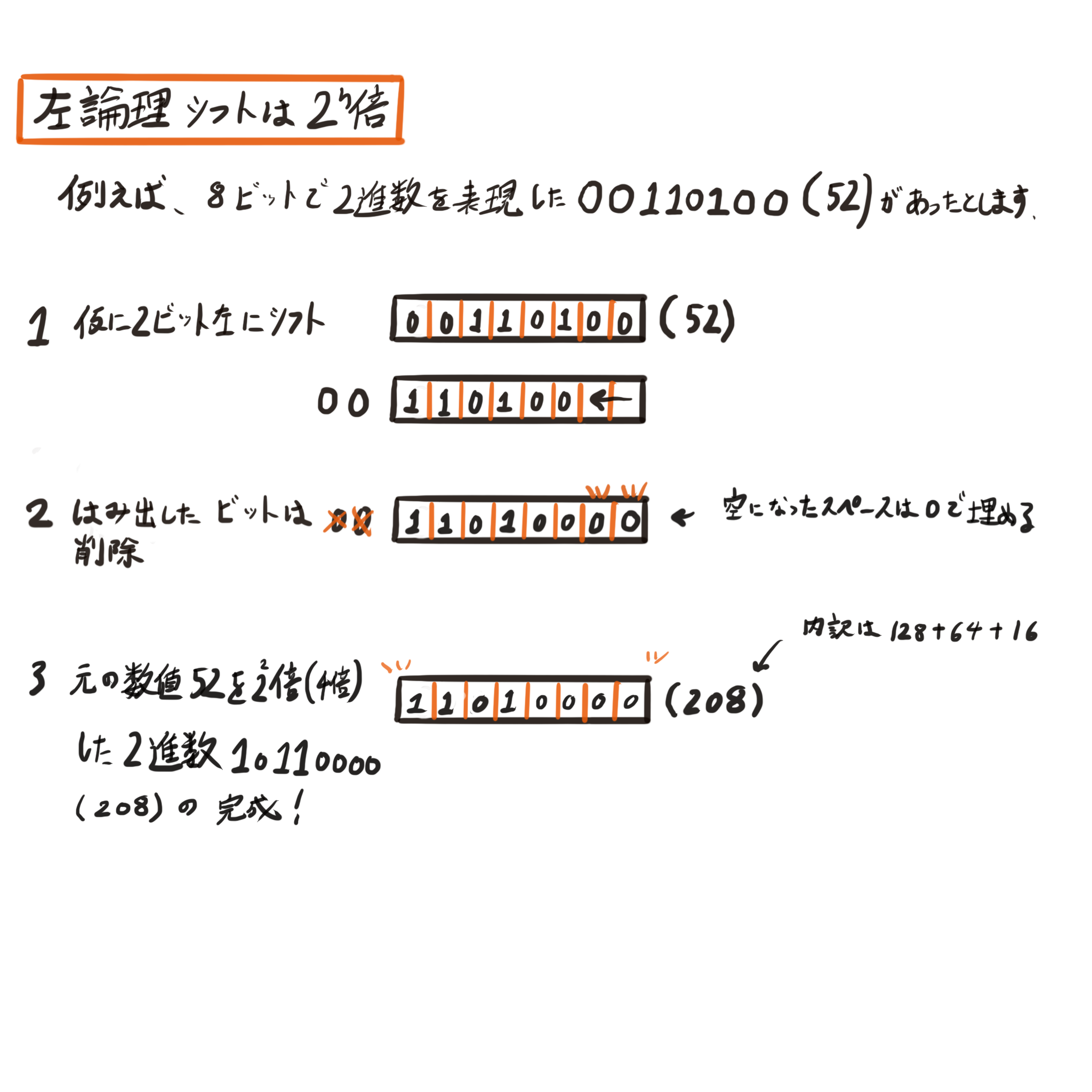
例えばこのデータを仮に2ビット左にシフトすると2²倍した2進数になります。
右論理シフト
符号を考慮せずにビット列全体を右にずらすのが右論理シフトです。
ずらしたビット数をnとすると、シフト後の数は元の数を1/2ⁿ倍したものになります。

例えばこのデータを仮に2ビット右にシフトすると1/2²倍した2進数になります。
ビットをずらした結果1が左右にはみ出した時はどうするの?
1が左右にはみ出した時にはそれぞれ次のような意味があります。
まず、左論理シフトではみ出した場合、演算の結果そのビット数で表現できる範囲を超えてしまったことになります、

また、この現象をオーバーフローと言います。
次に、右論理シフトではみ出した場合の数字は割り算した結果の余りということになります。
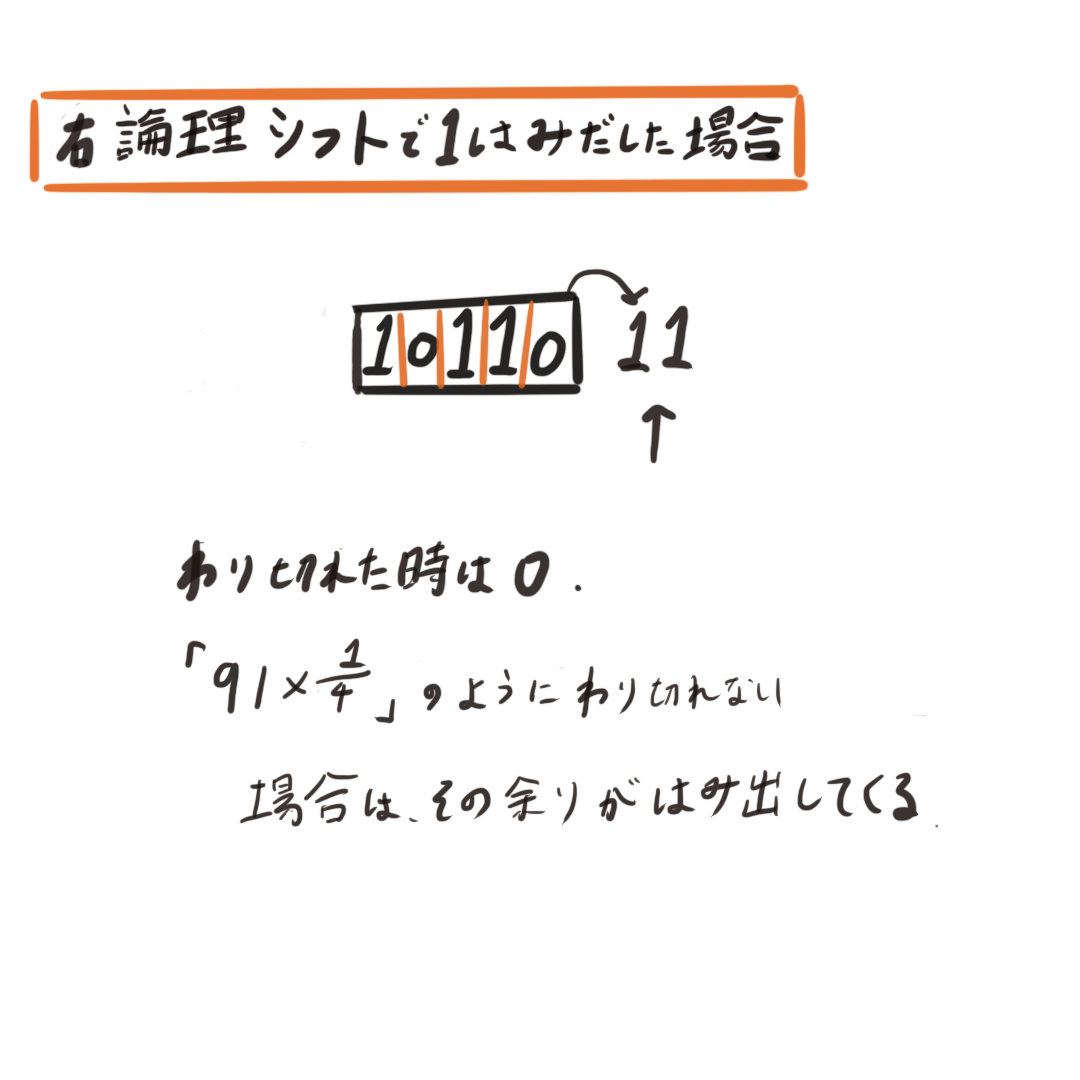
割り切れた時は0ですが、例えば94✖️1/4のように割り切れない場合はその余りがはみ出してきます。
算術シフト
2つ目の算術シフトは、論理シフトと違い、符号を考慮して行うシフト操作です。
算術シフトでは、先頭の符号ビットを固定にして、それ以降のビットだけを左右にシフト操作します。
左算術シフト
符号を考慮して、ビット列全体を左にずらすのが左算術シフトです。
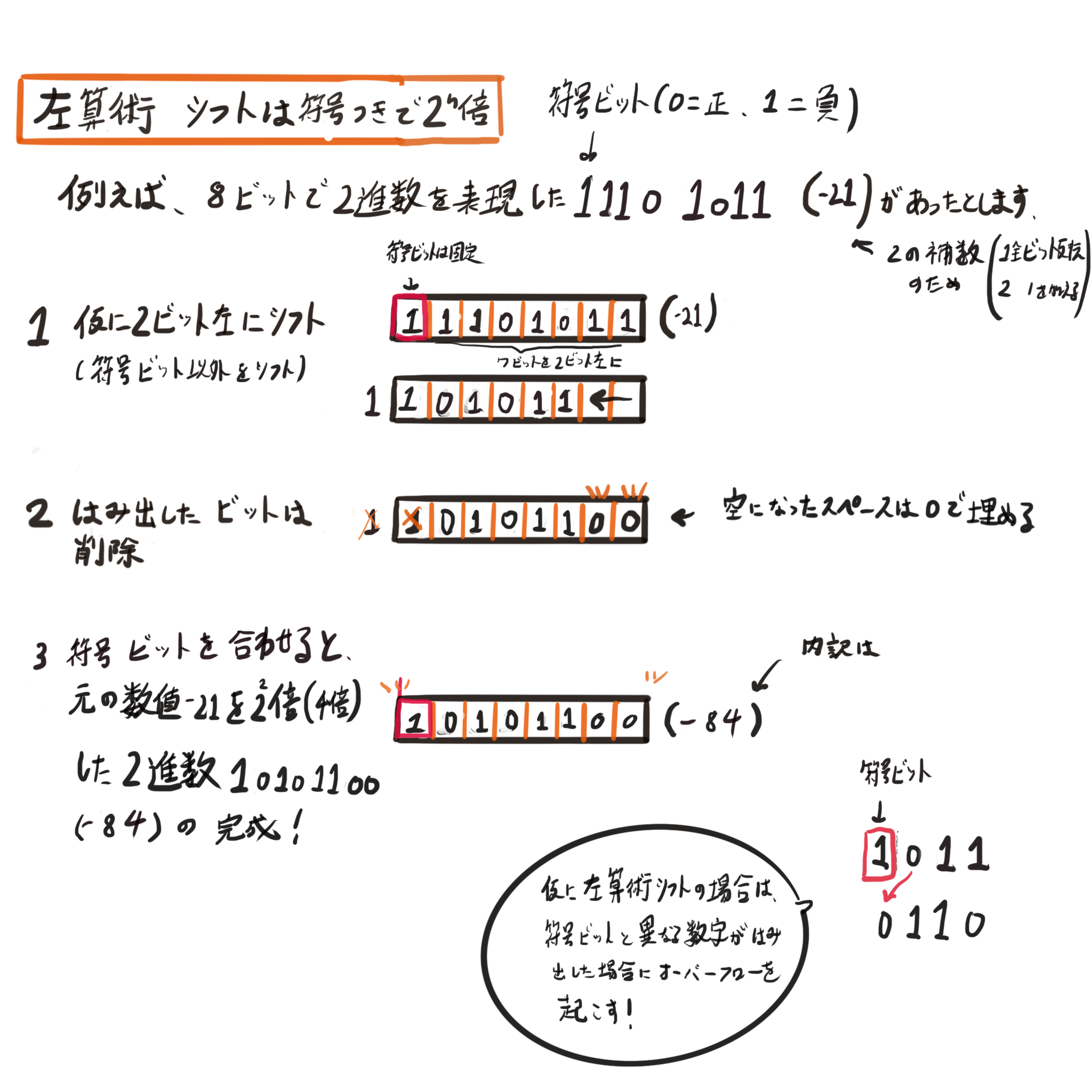
算術シフトも論理シフトと同じで左にずらすと2ⁿ倍になる基本は変わりません。
右算術シフト
符号を考慮して、ビット列全体を右にずらすのが右算術シフトです。
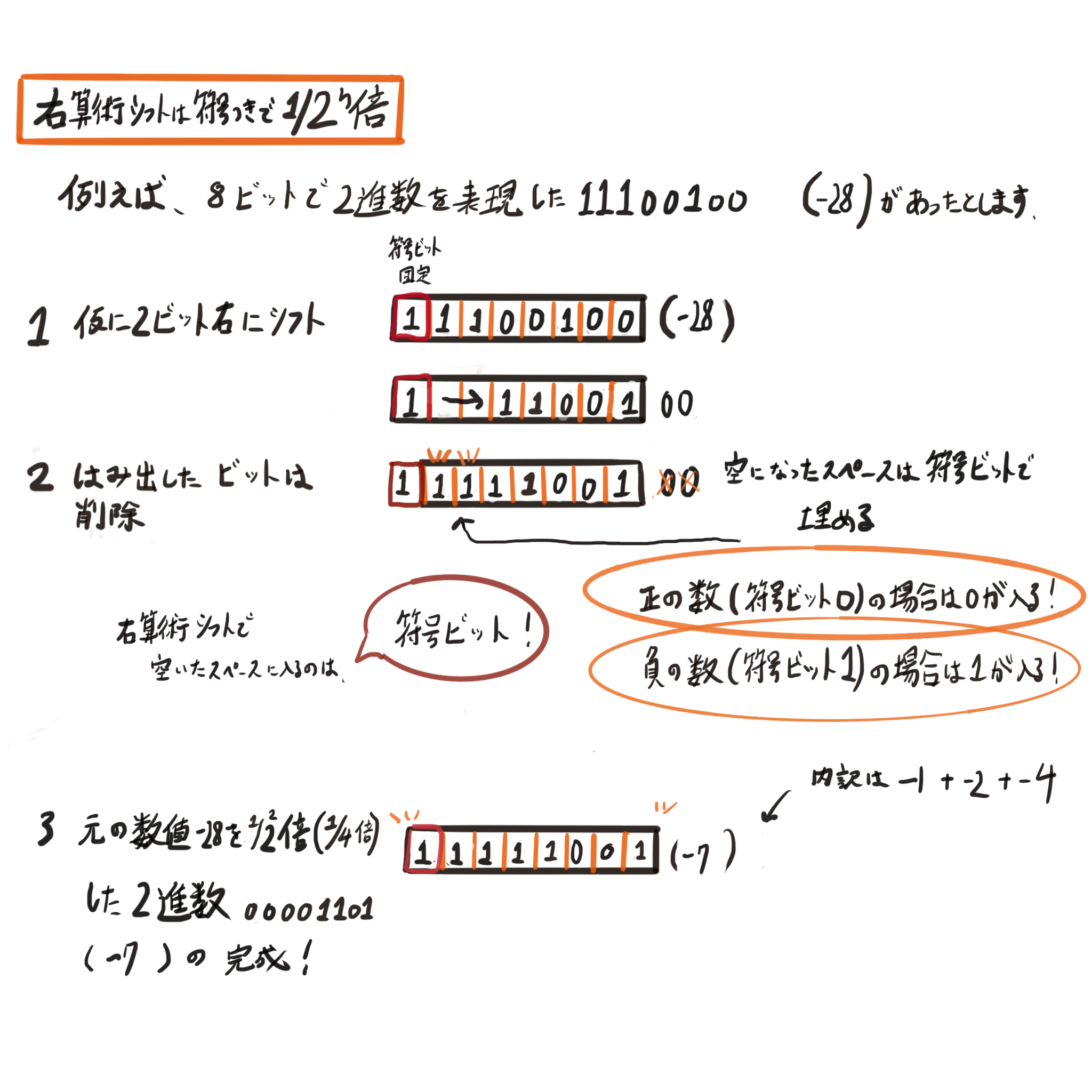
こちらも論理シフトと同じで、右にずらすと1/2ⁿ倍したものになるという基本は変わりません。
ただし、開いたビットを何で埋めるかは注意が必要で、0の決め打ちではなく、符号ビットになります。
正の数の場合は0が入り、負の数の場合は1が入るといった感じですね。
かけ算とわり算を理解する
これまで紹介したシフト演算を使ってコンピュータはかけ算やわり算を行っています。
しかし、単純に考えるとシフト演算では「2、4、8、16・・・」のような2ⁿにあたる数字でしか、かけ算も
割り算もできません。
「3」や「5」のように半端な数字で行う計算はどうすればいいのでしょうか?
かけ算、わり算のやり方をそれぞれみていきます。
かけ算の場合
まず、かけ算は2ⁿ同士の足し算に置き換えることによって半端な数字の計算もできるようにします。
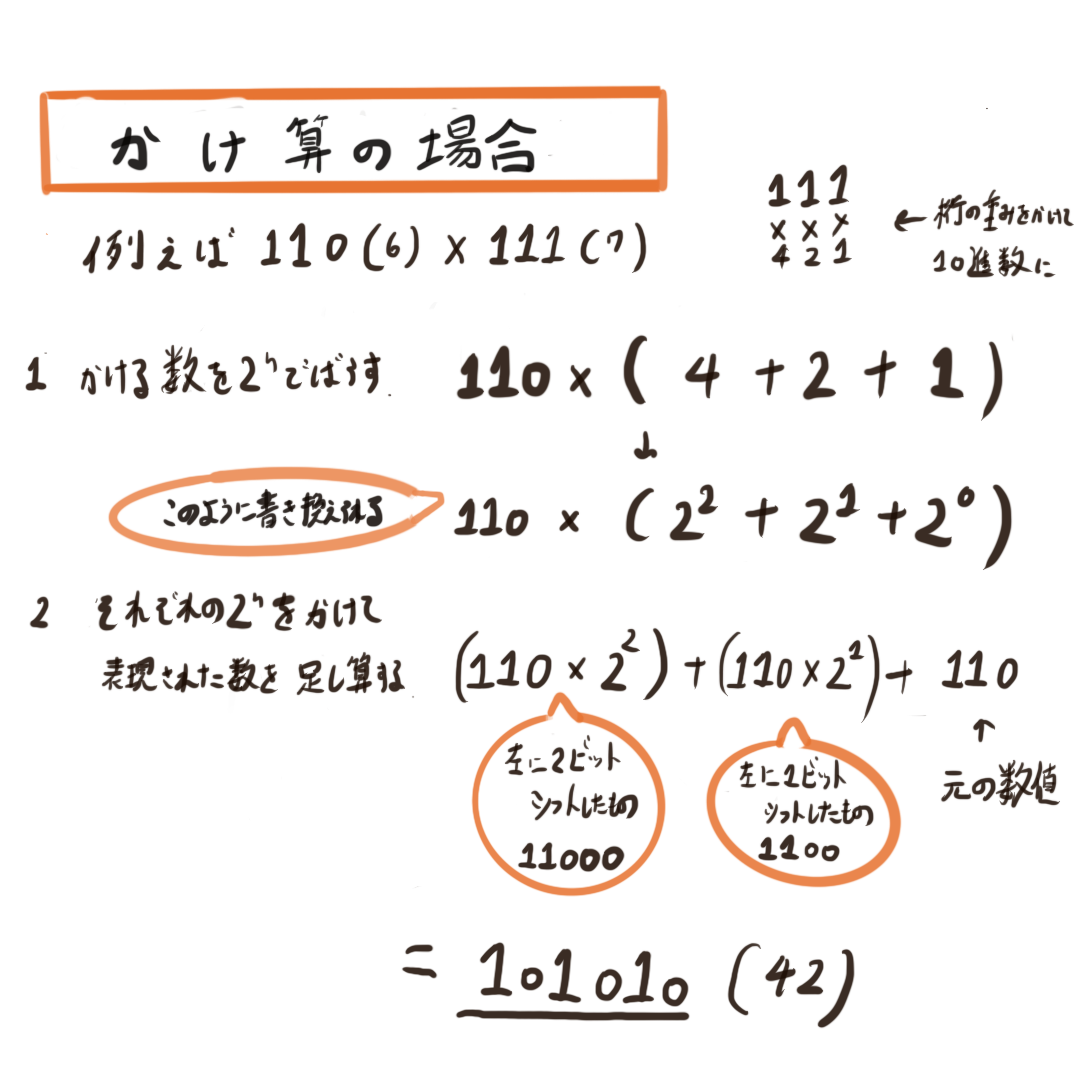
例えば、7倍だと2ⁿであらわせる数にばらすことによってそれぞれのシフトした数値を表現できます。
そして、最後に各シフトした数値を足し算することによってかけ算の結果が成立します。
わり算の場合
一方のわり算も基本は同じですが、わり算って何というところから整理する必要があります。
まず、割り算は分割できる数の計算であると言う前提を理解することが大切です。
例えば、15➗5は5ずつ3つに分けられるという意味です。
その前提を踏まえた上で、これを引き算の考え方で置き換えると、15という数字から5を3回引くことができるとみなすことができます。
今回の割り算はこの引き算の考え方を用いた2ⁿの引き算によって計算を行います。
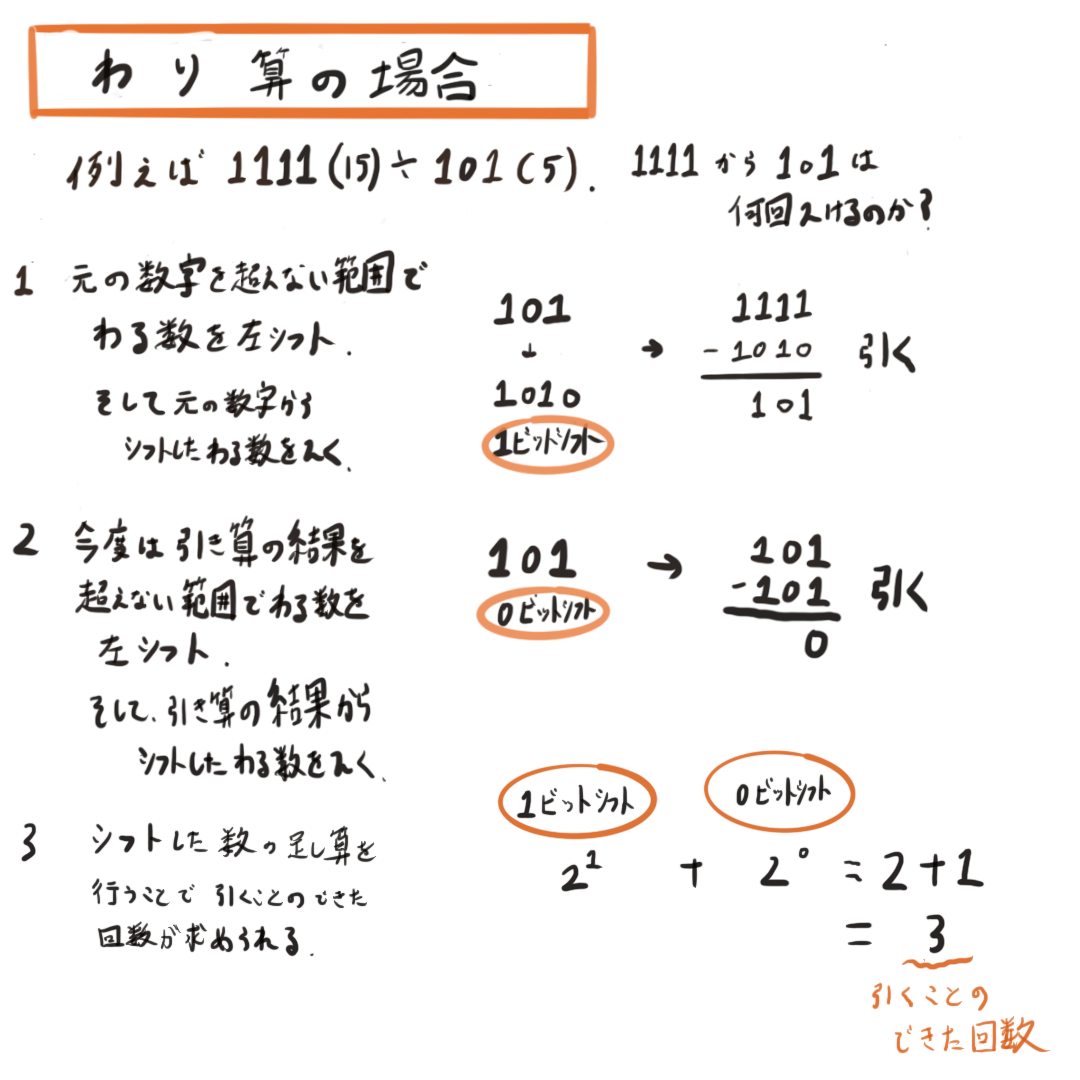
例えば、1111から101を引く数を求めるとするならば、まず元の数値を超えないようにわる数をシフトして引き算することを結果が0になるまで行います。
その結果がでたら、0になるまでにシフトした2ⁿをそれぞれ足すことによってわり算の結果が成立するのです。

また、この筆算のイメージができればコンピュータの割り算の理解にも役立ちます。
最後に

本日はシフト演算と2進数のかけ算とわり算についてというテーマでお送りしました。
冒頭にも紹介しましたが、今回の内容に関しては以下の本で学ばせてもらったことを参考にアウトプットさせていただいています。
こちらは基本情報技術者試験の参考書となっていますが、ITサイエンスの基礎を学んでいく上でおすすめの本です。
Amazon内の評価も高く、他にも参考書はありますが、文章メインではなくイラストが多用されているので、特に初学者の方にはとっつきやすく理解しやすいと思います。
ぼくもこの本にかなりお世話になっていて、おすすめできる書籍となっているので、気になる方はぜひ手にとってみてください。
それでは本日もありがとうございました。
今日も頑張ります。
[kanren postid=”3968,3894,3924,3937,3951,4003″]
